जब भी किसी भिन्न को हल करना हो चाहे भिन्न का जोड़ हो या घटाना तब इन प्रकार की भिन्नों को हल करने के लिए हमें भिन्नों के हरों का लघुत्तम समापवर्तक निकालना ही पड़ता है। ऐसा क्या कारण है कि ऐसा होता है।
इस पोस्ट में हम इसी के बारे में बड़ी ही सरलता से यह जानने वाले हैं कि भिन्नों को हल करते समय इनका लघुत्तम समापवर्तक ( ल. स. ) क्यों निकालना आवश्यक होता है।
हम भिन्नों को बिना ल.स निकाले भी हल कर सकते हैं पर केसे हम इसी पोस्ट में जानेंगे पर पहले ल. स का कारण जान लेते हैं। आइए आगे पढ़ते हैं >>>
इसको अच्छी तरह से समझने के लिए हमें कई उदाहरणों को सामिल करना होगा।
इस में हमें हर ( 5 व 7 ) का ल.स. निकालना पड़ेगा पर क्यों चलिए इसका मूल कारण देखते हैं।
हम देख रहे हैं कि 5 और 7 दोनों अलग अलग संख्याएँ हैं। सबसे पहले इन दोनों हरों को एकसमान संख्या में बदलना होगा तभी हम काॅमन ले सकते हैं। अगर ल.स की बात करें तो इनका ( 5 और 7 का ) ल.स 35 होगा। अब इसी 35 का गुणा और भाग दोनों भिन्नों के अंश व हर में करना होगा। गुणा करने के बाद भिन्नों का नया रुप इस तरह से होगा -
( 4 × 35 ) / ( 5 × 35 ) + ( 6 × 35 ) / ( 7 × 35 )
= ( 4 × 35 ) / ( 5 × 35 ) + ( 6 × 35 ) / ( 7 × 35 )
= ( 4 × 7 ) / 35 + ( 6 × 5 ) / 35
= 28 / 35 + 30 / 35, अब हम देख रहे हैं कि दोनों भिन्नों का हर एकसमान ( 35 ) हो गया है तो हम इसे काॅमन लेकर बाहर कर सकते हैं।
काॅमन लेने पर- 1/ 35 ( 28 + 30 )
= ( 1/ 35 ) × 58
= 58 / 35. उत्तर
तो देखा आपने हमें ल.स इसलिए लेना पड़ता है क्योंकि भिन वाला भाग ( हिस्सा ) अलग हो जाए और आसानी से जोड़ा जा सके । चलिए इसी सवाल को दूसरी तरह से समझते हैं।
4 / 5 + 6 / 7 की दोनों भिन्नों के हरों को किसी भी तरह से हमें बराबर करना है फिर उसके बाद इनका हल बहुत आसान हो जाएगा। तो आईए देखते हैं -
हम देख रहे हैं कि दोनों भिन्नों के हर 5 और 7 हैं। पहली भिन्न के अंश व हर में 7 का और दूसरी भिन्न के अंश व हर में 5 का गुणा करने पर -
( 4 × 7 ) / ( 5 × 7 ) + ( 6 × 5 ) / ( 7 × 5 )
= 28 / 35 + 30 / 35
= 1 / 35 ( 28 + 30 ) ( 1/35 काॅमन लेने पर )
= 58 / 35 = 1.6571 उत्तर
हम देख रहे हैं कि दोनों ही तरिकों में हमें भिन्नों के हरों को बराबर इसलिए करना होता है कि इन्हें अलग किया जा सके। एक तरिका ऐसा भी है जिसमें यह सब नहीं करना पड़ता है। कहने का मतलब है कि ना ही भिन्नों का ल.स निकालना पड़ता है या फिर हरों को बराबर करने की भी कोई आवश्यकता होती है। यह तरीका है भाग विधि जी हाँ हम भाग विधि से भी भिन्नों को हल कर सकते हैं।
चलिए हम 4 / 5 + 6 / 7 इसी भिन्न को लेकर देखते हैं।
पहली भिन्न 4/5 = 0.8 ( भाग करने पर )
दूसरी भिन्न 6/7 = 0.85714 ( भाग करने पर )
दोनों मानों को जोड़ने पर - 0.8 + 0.85714 = 1.6571
इस तरह हम देख रहे हैं कि भिन्नों को जोड़ने या घटाने के लिए इनके हरों का लघुत्तम समापवर्तक हरों को एकसमान करने के लिए निकाला जाता है ताकि भिन्न और साधारण जोड़ या घटाना अलग अलग हों जाएँ और आसानी से हल हो जाए।
ये जानकारी आपको कैसी लगी इसके बारे में कमेंट जरुर करें। धन्यवाद..
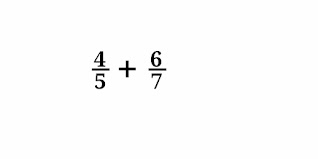




0 टिप्पणियाँ